
Written by: Simone Cantori, Emanuele Costa, Giuseppe Scriva, Luca Brodoloni, Sebastiano Pilati, from the University of Camerino
Predicting the properties of complex quantum systems is one of the central problems in condensed matter physics and quantum chemistry. Classical computers appear to be intrinsically unsuited for this task. Indeed, just representing the quantum system’s state requires resources that scale exponentially with the system’s size. On the other hand, rather than solving the fundamental laws of quantum physics in a deductive approach, one could bypass the exact solution and follow an inductive approach based on data. This points to the use of machine learning algorithms, possibly based on deep neural networks. As probably already known to the reader, deep learning has emerged in recent years as an astonishingly powerful approach to tackling commercially relevant problems in computer vision and language processing. Unsurprisingly, these techniques are rapidly being adopted in various branches of quantum science, particularly for the simulation of electronic structures [1]. However, while the training data are abundant in the context of classical computational tasks, data describing quantum systems are scarcer and unavoidably incomplete. Such data could be generated via classical computer simulations, but this brings us back to the deductive approach, and it is thus feasible only for small systems. In this respect, scalability emerges as a fundamental property of the neural networks employed in the quantum domain. If scalable, a network can be trained on a computationally accessible size and then used to predict the properties of larger, computationally prohibitive systems. So far, if and to what extent such extrapolations remained accurate was unknown. This is indeed one of the main questions addressed in this PRACE-ICEI project.
From the above discussion, another question naturally arises: can we use quantum devices to produce the data needed to train deep neural networks? Could these data allow neural networks to solve otherwise intractable computational tasks? In fact, some formal guarantees on the accuracy in ground-state property prediction have recently been reported [2]. Yet, the application of this approach to experimentally relevant models needs further investigation. Several experimental platforms, including Rydberg atoms in optical tweezers, trapped ions, or devices built with superconducting-flux qubits, are being developed to perform quantum simulations of classically intractable models. For this PRACE-ICEI project, we explored the use of quantum annealers from D-Wave Systems Inc., which we accessed via an ISCRA Cineca project. The spin configurations sampled by the quantum annealer have been used to accelerate the Monte Carlo simulations of spin glasses, representing a well-known hard computational task.
Below we report some details on the use of the HPC resources provided through the PRACE-ICEI proposal and on the parallelization strategy. Then, some of our specific research endeavours are highlighted, including the prediction of ground-state properties of disordered quantum systems, the emulation of universal quantum circuits, the acceleration of spin-glass simulations, and the development of universal energy functionals for density function theory.
Utilization of HPC resources
Most of our training datasets were produced via exact diagonalization routines or by running quantum Monte Carlo (QMC) simulations. In the first case, well-developed codes exist, e.g., from the MKL Intel library, and these efficiently exploit multi-core CPUs. For the QMC simulation, share-memory parallelism was exploited to distribute the execution of several stochastic walkers on different CPU cores. Notably, the training of deep neural networks can be performed via popular deep-learning frameworks, chiefly PyTorch and TensorFlow. These efficiently exploit GPU accelerators, including multi-GPU configurations. This stems from the massive parallelism allowed when backpropagation is applied to batches of training instances. Access to the Fenix infrastructure was granted through the PRACE-ICEI call for proposals (V04).
Scalable neural networks for quantum systems
Since training data can be (classically) produced only for relatively small quantum systems, supervised learning turns out to be practically useful only when performed using scalable architectures. This way, the trained network might be able to simulate larger systems than those present in the training set. We implemented scalable architectures including global pooling layers [3, 4], as schematically shown in Fig. (1), or, for extensive properties, including only convolutional layers (see discussion on density functional theory below [5]).
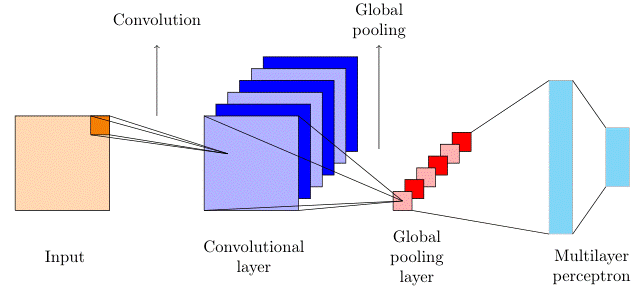
Emulating quantum circuits
Predicting the output of gate-based universal quantum computers is an extremely challenging computational task. It is needed to test and further develop existing quantum devices, and it also serves as a benchmark of computational efficiency to justify claims of quantum advantage. We explored if and to what extent supervised learning allows deep networks to predict single and two-qubit output expectation values [4]. A proper one-hot encoding of a set of single-qubit and two-qubit gates was fed as network input [see Fig. (2)]. Interestingly, in various cases, the predictions can be extrapolated to larger qubit numbers while increasing the circuit depth appears to be more challenging.
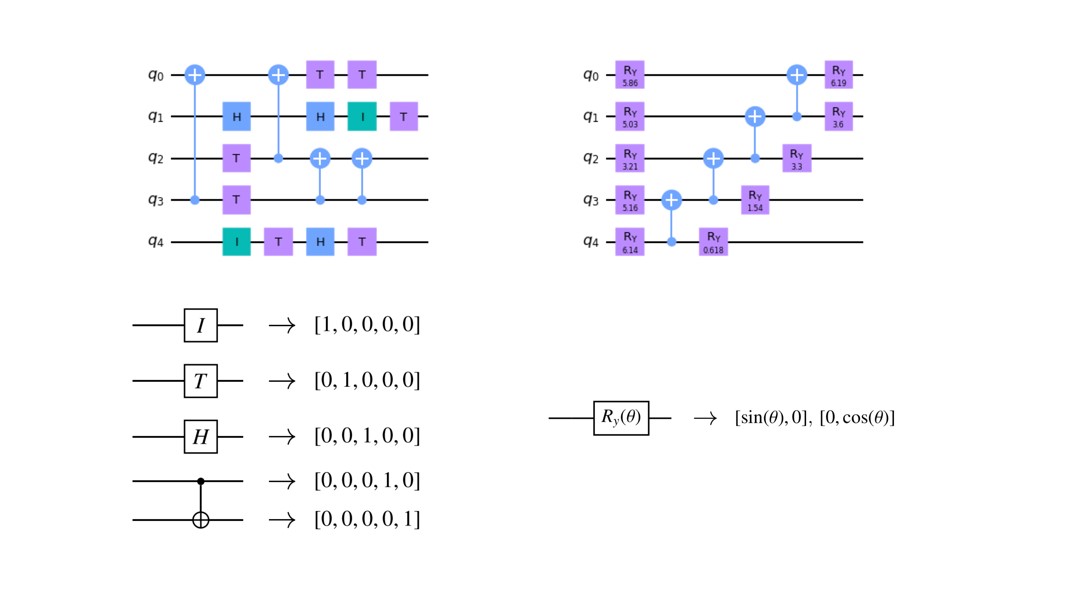
Learning universal functionals
Density functional theory posits that ground-state properties can be derived from a reduced set of observables: the density profiles (in the case of continuous space systems) or the single-spin magnetizations (for quantum spin models). While this allows bypassing the exponential-scaling obstacle described above, the universal functional is unknown. We used deep neural networks to learn such functional from data, considering continuous-space models for cold-atoms in optical speckle potentials [6] and random quantum Ising models [5]. In the latter case, the output is an extensive set of expectation values, and scalability was implemented using only convolutional layers [see Fig. (3)].
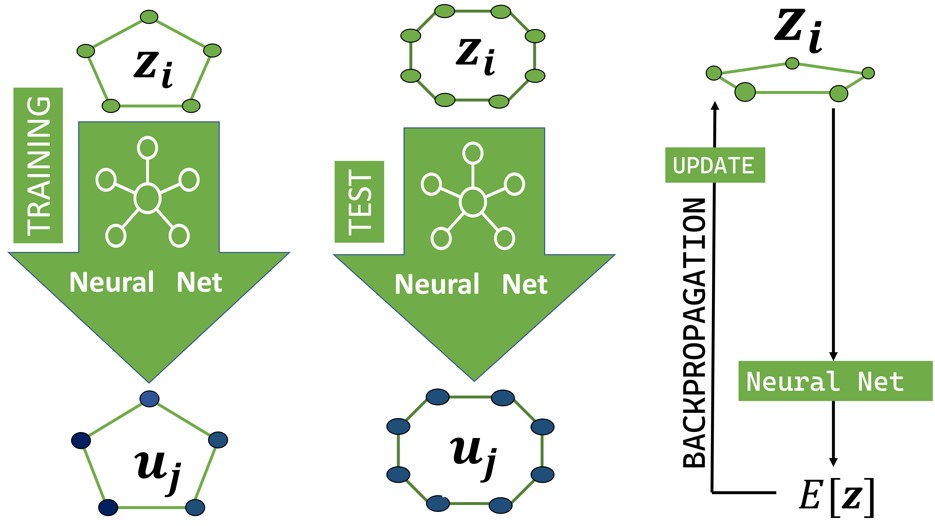
Accelerating spin-glass simulations
Quantum annealers are routinely used to tackle hard combinatorial optimization problems. They allow sampling low-energy spin configurations of challenging spin-glass models. Recently, at UniCam we have shown that autoregressive neural networks allow accelerating Markov chain Monte Carlo simulations of spin glasses. However, the networks need low-energy configurations for training. For this PRACE-ICEI project, we have shown that suitable configurations can be generated using a D-Wave quantum annealer [7]. A hybrid neural algorithm was implemented, and this turned out to be competitive with parallel tempering, with the benefit of a much faster thermalization.
Resilience to noise
Quantum devices such as, e.g., Rydberg-atom arrays or annealers based on superconducting qubits, might be used to produce training data for neural networks. However, quantum devices are unavoidably unaffected by shot noise and by other sources of errors. Interestingly, we have seen that deep neural networks are remarkably resilient to noise in the training data. For example, random distortions in the target ground-state energy, or shot noise in the output of quantum circuits [4], are efficiently filtered out. This means that deep networks are able to correct random errors present in the training data. This observation gives strong support to the perspective of using quantum devices as data generators for deep learning.
References:
[1] H. J. Kulik et al., Roadmap on Machine learning in electronic structure, Electronic Structure 4, 023004 (2022) https://dx.doi.org/10.1088/2516-1075/ac572f
[2] Hsin-Yuan Huang et al., Provably efficient machine learning for quantum many-body problems, Science 377, eabk3333 (2022) https://doi.org/10.1126/science.abk3333
[3] N. Saraceni, S. Cantori, S. Pilati, Scalable neural networks for the efficient learning of disordered quantum systems, Physical Review E 102, 033301 (2020) https://doi.org/10.1103/PhysRevE.102.033301
[4] S. Cantori, D. Vitali, S. Pilati, Supervised learning of random quantum circuits via scalable neural networks, Quantum Science and Technology 8, 025022 (2023) https://dx.doi.org/10.1088/2058-9565/acc4e2
[5] E. Costa, R. Fazio, S. Pilati, Deep learning non-local and scalable energy functionals for quantum Ising models, arXiv:2305.15370 (2023) https://doi.org/10.48550/arXiv.2305.15370
[6] E. Costa, G. Scriva, R. Fazio, S. Pilati, Deep-learning density functionals for gradient descent optimization, Physical Review E 106, 045309 (2022), https://doi.org/10.1103/PhysRevE.106.045309
[7] G. Scriva, E. Costa, B. McNaughton, S. Pilati, Accelerating equilibrium spin-glass simulations using quantum annealers via generative deep learning, SciPost Physics (in press, 2023) https://doi.org/10.48550/arXiv.2210.11288
Acknowledgments
We thank PRACE for awarding access to the Fenix Infrastructure resources at Cineca, which are partially funded by the European Union’s Horizon 2020 research and innovation program through the ICEI project under the Grant Agreement No. 800858. Furthermore, we acknowledge the Cineca award under the ISCRA initiative, for providing access to D-Wave quantum computing resources and for support. Our research was also partially supported by the PNRR MUR project PE0000023-NQSTI.